Выпуклый многоугольник

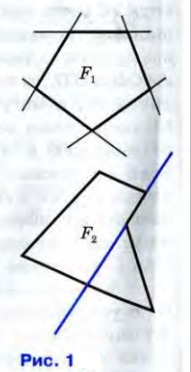Многоугольник называется выпуклым, если  он лежит по одну сторону от каждой прямой,проходящей через две его соседние вершины.

На рисунке 1 многоугольник F₁ является выпуклым,а многоугольник F₂ — невыпуклым.

Сумма углов выпуклого n-угольника равна (n-2) *180° .

Доказательство:

Рассмотрим выпуклый n-угольник , изображенный на рисунке 2,a. Углы  A_nA₁A₂ , A₁A₂A₃ ,  ...., A_n-1A_nA₁ называются углами этого многоугольника.Найдем их сумму.
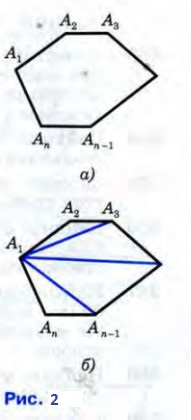Для этого соединим диагоналями вершину A₁ c другими вершинами.В результате получим n -2 треугольника (рис 2,а),сума углов которых равна сумме углов n -угольника. Сумма углов каждого треугольника равна 180°,поэтому сумма углов многоугольника A₁A₂ ... A_n равна (n-2) *180°. 

Внешним углом выпуклого n-угольника называется угол ,смежный с углом многоугольника.

Сумма внешних углов выпуклого многоугольника равна 360°. 

Доказательство:

Если при каждой вершине выпуклого многоугольника A₁A₂ ... A_n взять по одному внешнему углу, то сумма этих внешних углов окажется равной:

180° - A₁ + 180° - A₂  + ... + 180 - A_n =

n * 180° - (A₁ + A₂ + ... A_n ) =

n * 180° - (n-2) * 180°- (n - 2) * 180° =    360° .