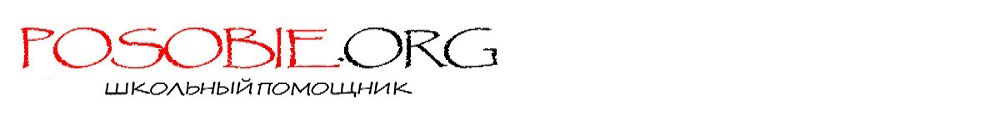Параллелограмм

Определение:

Параллелограмм - четырехугольник,у которого противоположные стороны попарно параллельны.

На рисунке 1 изображен параллелограмм ABCD: AB  ∥ CD, AD ∥ BC.

Параллелограмм является выпуклым четырехугольником .

Свойства параллелограмма:

1. В параллелограмме противоположные стороны равны  и противоположные  углы равны.

Доказательство:

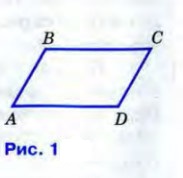
Рассмотрим параллелограмм ABCD (рис 2). Диагональ AC разделяет его на два треугольника: ABC и ADC. Эти треугольнике равны по стороне и двум прилежащим углам(AC - общая сторона , ∠ 1 = ∠ 2 и ∠ 3 =∠ 4 как накрест лежащие углы при пересечении  секущей AC параллельных прямых AB и CD, AD и BC.

Поэтому AB = CD ,AD = BC и ∠B = ∠ D

Далее,пользуясь равенством углов 1 и 2, 3 и 4, получаем ∠A = ∠1+∠3=∠2+∠4=∠C

2.Диагонали параллелограмма точкой пересечения делятся пополам.

Доказательство:

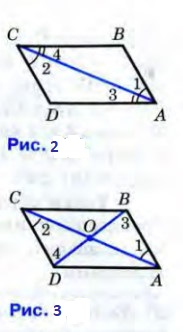
Пусть О - точка пересечения диагоналей AC и BD параллелограмма ABCD (рис 3). Треугольники AOB и COD равны по стороне и двум прилежащим углам (AB = CD как противоположные стороны параллелограмма, ∠1 = ∠2 и ∠3 = ∠4 как накрест лежащие углы при пересечении параллельных прямых AB и CD секущими AC и  BD соответственно). Поэтому AO = OC,OB = OD, что и требовалось доказать.

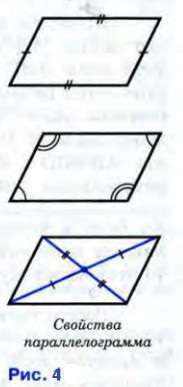
Рисунок 4 иллюстрируют все рассмотренные свойства .